Los números primos se empiezan a estudiar en el último ciclo de Primaria para empezar a comprender conceptos de divisibilidad. A veces nos preguntamos para qué sirven en realidad los números primos, así que aquí vamos a ver cuáles son algunas de sus utilidades.
Antes que nada, vamos a ver qué son los números primos.
Índice
¿Qué son los números primos?
Los números primos son todos aquellos que solamente son divisibles por sí mismos y por 1. Al resto, los números que pueden dividirse por más números, además de uno y sí mismos (siendo una división exacta), se les denomina números compuestos.
Los primos se encuentran entre los números más importantes de las matemáticas y son infinitos, como lo son los números.
Los números primos son enormemente importantes, al ser la base sobre la que se construyen códigos y se calculan algoritmos complejos para, por ejemplo, la criptografía. Pero nosotros no vamos a utilizarlos para cuestiones tan complejas, sino que vamos a buscar sus utilidades en operaciones sencillas que podemos utilizar a diario
Utilidades de los números primos: Hallar el Mínimo Común Múltiplo y el Máximo Común Divisor
Los números primos nos sirven para realizar algunas operaciones matemáticas, por ejemplo para hallar el Mínimo Común Múltiplo (m.c.m) y el Máximo Común Divisor (m.c.d.). Sobre todo nos resultarán muy útiles cuando estemos buscando el m.c.m y el m.c.d de números mayores.
Aquí tenemos dos videos de ejemplo de cómo usar los números primos para hallar el m.c.m y el m.c.d.
¿Cómo hallar los números primos?
Veamos cómo encontrar los números primos. Para empezar, sacaremos de los primos el número 1, que ni se considera primo ni tampoco compuesto, como es evidente.
En los números hasta el 10, sabemos que son primos el 2, el 3, el 5 y el 7. Estos cuatro números son divisibles solo por 1 y por sí mismos.
La dificultad para encontrar un número primo está en aquellos que comienzan a tener más de dos cifras, porque en un primer vistazo puede resultar complicado saber si son divisibles sólo por 1 y por sí mismos.
Pero hay soluciones, ‘TRUCOS’ que nos ayudarán a saber si un número es primo.
Esos trucos se llaman Criterios de Divisibilidad.
Aplicar Criterios de Divisibilidad
La DIVISIBILIDAD de un número es la condición por la cual un número dividido por otro tiene como resto 0.
>> Son divisibles por 2 todos los números pares. Al dividirlos por 2 su resto es 0.
-
– 48 es divisible por 2 porque es par. Si lo dividimos entre 2, su resto nos dará 0. Es una división exacta.
>> Son divisibles por 3 los números que al dividirlos entre 3 dan como resto 0.
-
– 63 es divisible por 3 porque es un múltiplo de 3. Si lo dividimos entre 3, veremos que su resto es 0. Es una división exacta.
Y así con el resto de las REGLAS DE DIVISIBILIDAD que veremos a continuación:
- Son DIVISIBLES POR 2: Todos los números pares.
- Son DIVISIBLES POR 3: Si la suma de sus cifras es múltiplo de 3.
- Son DIVISIBLES POR 4: Los acabados en 00 o si la suma de sus cifras es múltiplo de 4.
- Son DIVISBLES POR 5: Los acabados en 0 o 5.
- Son DIVISIBLES POR 6: Los divisibles por 2 y 3..
- Son DIVISIBLES POR 7: 7 es primo..
- Son DIVISIBLES POR 8: Los acabados en 000 o si la suma de sus cifras es múltiplo de 8.
- Son DIVISIBLES POR 9: Si la suma de sus cifras es múltiplo de 9.
Para saber rápidamente si un número es primo o no comprobaremos los Criterios de Divisibilidad
>> Hallando números primos
Partimos de varios números al azar.
-
* Ejemplo 2: 97
Divisible por 2: No, porque NO es par, por tanto no es divisible por 2.
Divisible por 3: No, porque la suma de sus cifras es 16, y 16 no es múltiplo de 3
Divisible por 4: Ni acaba en 00 ni en número par (no puede ser múltiplo de 4).
Divisible por 5: NO, porque ni acaba en 0 ni en 5.
Divisible por 6: No, porque no es divisible por 2 ni por 3.
Divisible por 8: Tampoco. Ni acaba en 000 ni es par, (no puede ser múltiplo de 8).
Divisible por 9: No. La suma de sus cifras, 16, no es un múltiplo de 9.
Ningún criterio de divisibilidad se cumple con el 97.
97 es un número primo
En números grandes, pongamos por ejemplo el 24.578, podemos aplicar igual los criterios de divisibilidad. Aunque también hay otras maneras: la criba de Erastótenes.
La Criba de Erastótenes
La Criba de Erastótenes es un procedimiento por el que podemos hallar todos los números primos hasta el número que queramos mediante el uso de una tabla.
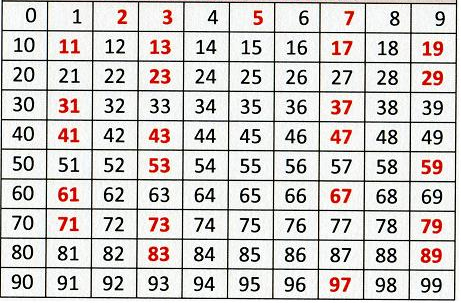
Para ello, colocaremos los números dentro de una tabla y partiendo de un número inicial quitaremos los múltiplos de 2, 3, 5 y 7. Los números que nos queden serán primos.
- Suprimimos el 1, porque, como ya hemos dicho, ni es primo ni compuesto.
- A continuación, partiendo del 2, que también excluiremos porque al ser divisible por sí mismo y por 1 ya sabemos que es primo, buscaremos todos los múltiplos de 2 y los marcaremos en negrita.
- Luego, seguiremos con el 3, que es primo por ser divisible por sí mismo y por 1 (no lo es por su anterior, el 2) y seleccionaremos todos sus múltiplos, que quedarán excluidos.
- Haremos lo mismo con el 5, que también es primo, pero quitaremos todos sus múltiplos.
- Y, finalmente, con el 7 repetiremos la misma operación, eliminando todos sus multiplos.
[/su_list]
Los números no marcados, que quedarán sin resaltar en negrita, son los números primos hasta el 100.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Así tenemos que hasta el 100 los números primos son:
2, 3, 5, 7, 11, 13, 17, 19, 23, 27, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,73, 79, 83, 89, 97.
Sabiendo que todos los múltiplos de 2, 3, 5 y 7 no son números primos, podremos decir que el número que hemos puesto en el ejemplo, el 24.578 no es primo, porque al terminar en 8 es divisible por 2 y por tanto NO ES PRIMO.
Si te ha gustado este artículo o te ha resultado útil, por favor, compártelo y valóralo.


 (14 votos, promedio: 4,57 de 5)
(14 votos, promedio: 4,57 de 5)